Soal Matematika Kelas 6 Tentang Bangun Datar dan Jawabannya

Matematika merupakan salah satu pelajaran yang memang tidak bisa dipisahkan dalam kehidupan sehari-hari. Salah satu materi yang akan dipelajari oleh siswa kelas 6 adalah bangun datar. Apa itu bangun datar? Bagaimana macam-macam bangun datar yang harus diketahui oleh siswa kelas 6? Yuk, mari simak ulasan di bawah ini!

Bangun datar adalah sebuah bentuk geometri dua dimensi yang terletak di bidang datar dan memiliki sisi-sisi yang tidak berukuran atau berbentuk garis lurus maupun lengkung. Contohnya adalah segitiga, segiempat, segilima, persegi panjang, trapesium, dan lain-lain.

Soal Matematika Kelas 6 Tentang Bangun Datar dan Jawabannya

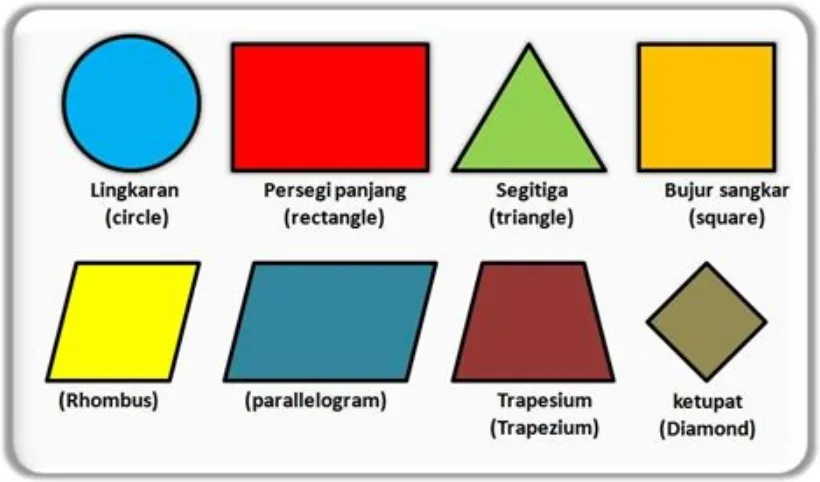
Nah, di bawah ini akan dijelaskan mengenai macam-macam bangun datar beserta sifat-sifatnya sehingga siswa kelas 6 bisa lebih memahami materi ini dengan baik.

1. Segitiga

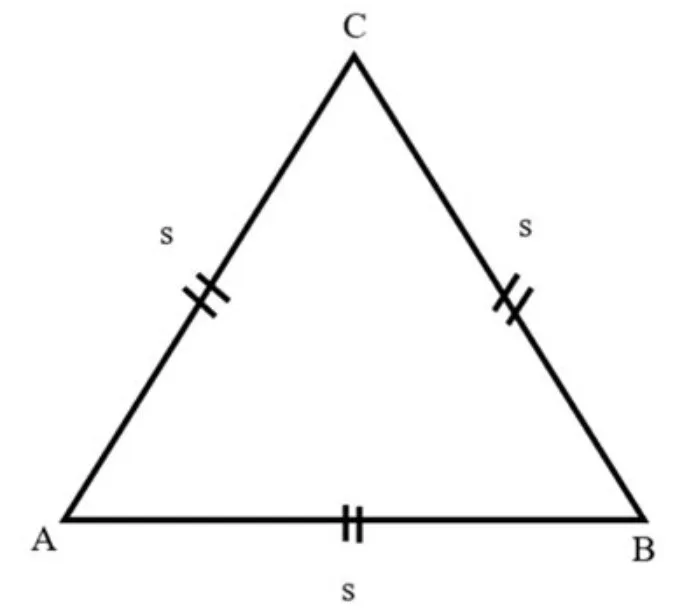
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Sifat-sifat segitiga adalah:

• Jumlah seluruh sudut dalam segitiga adalah 180 derajat.
• Segitiga memiliki beberapa jenis, yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
• Rumus luas segitiga adalah L = 1/2 x alas x tinggi.
• Rumus keliling segitiga adalah K = sisi 1 + sisi 2 + sisi 3.

Segitiga sama sisi memiliki sisi-sisi dengan panjang yang sama. Segitiga sama kaki memiliki dua sisi yang sama panjang. Sedangkan segitiga sembarang tidak memiliki sisi yang sama panjang dan sudut yang sama besar.

2. Segiempat

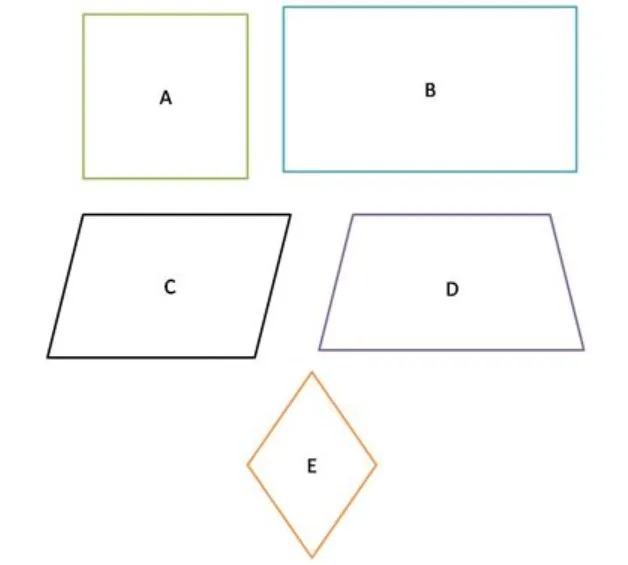
Segiempat adalah bangun datar yang memiliki empat sisi dan empat sudut. Sifat-sifat segiempat adalah:

• Jumlah seluruh sudut dalam segiempat adalah 360 derajat.
• Segiempat memiliki beberapa jenis, yaitu persegi, persegi panjang, layang-layang, dan belah ketupat.
• Rumus luas persegi adalah L = s^2, sedangkan rumus keliling persegi adalah K = 4 x s.
• Rumus luas persegi panjang adalah L = panjang x lebar, sedangkan rumus keliling persegi panjang adalah K = 2 x (panjang + lebar).
• Rumus luas layang-layang adalah L = 1/2 x diagonal 1 x diagonal 2, sedangkan rumus keliling layang-layang adalah K = 2 x (sisi 1 + sisi 2).
• Rumus luas belah ketupat adalah L = 1/2 x diagonal 1 x diagonal 2, sedangkan rumus keliling belah ketupat adalah K = 4 x sisi.

Persegi memiliki keempat sisinya sama panjang dan keempat sudutnya sudut siku-siku. Persegi panjang memiliki kedua sisi sejajar sama panjang dan keempat sudutnya sudut siku-siku. Layang-layang memiliki keempat sisinya sama panjang. Sedangkan belah ketupat memiliki keempat sisinya sama panjang dan kedua sudutnya sama besar.

Itulah tadi pengertian dan macam-macam bangun datar yang harus dipahami oleh siswa kelas 6. Semoga dengan memahami sifat-sifat dari masing-masing bangun datar tersebut, siswa dapat lebih mudah dalam menjawab soal matematika kelas 6 tentang bangun datar dan dapat mencapai hasil belajar yang lebih baik.

Perhitungan Luas dan Keliling Bangun Datar

Bangun datar merupakan bangun geometri yang memiliki dua dimensi yakni panjang dan lebar. Dalam menyelesaikan soal matematika kelas 6 tentang bangun datar, terdapat beberapa hal yang harus dipahami, salah satunya pertama kali adalah soal perhitungan luas dan keliling bangun datar. Berikut ini akan dijelaskan secara detail mengenai perhitungan luas dan keliling bangun datar.

Perhitungan Luas Bangun Datar

Luas bangun datar merupakan luas wilayah yang diarsir pada bidang datar oleh bangun tersebut. Setiap bangun datar mempunyai rumus luas yang berbeda-beda. Berikut ini akan dijelaskan cara menghitung luas dari masing-masing bangun datar:

Persegi

Untuk menghitung luas persegi, rumus yang digunakan adalah S^2, dimana S adalah panjang sisi persegi yang mempunyai nilai sama semua.

Contoh soal: Sebuah persegi memiliki panjang sisi 6 cm. Tentukanlah luas dari persegi tersebut!

Jawab: S^2 = 6^2 = 36. Jadi, luas persegi tersebut adalah 36 cm^2.

Persegi Panjang

Untuk menghitung luas persegi panjang, rumus yang digunakan adalah p x l atau panjang dikali lebar.

Contoh soal: Sebuah persegi panjang memiliki panjang 5 cm dan lebar 3 cm. Tentukanlah luas dari persegi panjang tersebut!

Jawab: p x l = 5 x 3 = 15. Jadi, luas persegi panjang tersebut adalah 15 cm^2.

Lingkaran

Untuk menghitung luas lingkaran, rumus yang digunakan adalah πr^2, dimana π adalah konstanta yang bernilai 3,14 dan r adalah jari-jari lingkaran.

Contoh soal: Sebuah lingkaran memiliki jari-jari 4 cm. Tentukanlah luas dari lingkaran tersebut!

Jawab: πr^2 = 3,14 x 4^2 = 3,14 x 16 = 50,24. Jadi, luas lingkaran tersebut adalah 50,24 cm^2.

Segitiga

Untuk menghitung luas segitiga, rumus yang digunakan adalah 1/2 x t x a, dimana t adalah tinggi segitiga dan a adalah alas segitiga.

Contoh soal: Sebuah segitiga mempunyai alas 8 cm dan tinggi 4 cm. Tentukanlah luas dari segitiga tersebut!

Jawab: 1/2 x t x a = 1/2 x 4 x 8 = 16. Jadi, luas segitiga tersebut adalah 16 cm^2.

Perhitungan Keliling Bangun Datar

Keliling bangun datar merupakan jumlah panjang sisi pada bangun tersebut. Setiap bangun datar mempunyai rumus keliling yang berbeda-beda. Berikut ini akan dijelaskan cara menghitung keliling dari masing-masing bangun datar:

Persegi

Untuk menghitung keliling persegi, rumus yang digunakan adalah 4 x S, dimana S adalah panjang sisi persegi yang mempunyai nilai sama semua.

Contoh soal: Sebuah persegi memiliki panjang sisi 6 cm. Tentukanlah keliling dari persegi tersebut!

Jawab: 4 x S = 4 x 6 = 24. Jadi, keliling persegi tersebut adalah 24 cm.

Persegi Panjang

Untuk menghitung keliling persegi panjang, rumus yang digunakan adalah 2 x (p + l) atau dua kali jumlah panjang dan lebar.

Contoh soal: Sebuah persegi panjang memiliki panjang 5 cm dan lebar 3 cm. Tentukanlah keliling dari persegi panjang tersebut!

Jawab: 2 x (p + l) = 2 x (5 + 3) = 16. Jadi, keliling persegi panjang tersebut adalah 16 cm.

Lingkaran

Untuk menghitung keliling lingkaran, rumus yang digunakan adalah 2 x π x r, dimana π adalah konstanta yang bernilai 3,14 dan r adalah jari-jari lingkaran.

Contoh soal: Sebuah lingkaran memiliki jari-jari 4 cm. Tentukanlah keliling dari lingkaran tersebut!

Jawab: 2 x π x r = 2 x 3,14 x 4 = 25,12. Jadi, keliling lingkaran tersebut adalah 25,12 cm.

Segitiga

Untuk menghitung keliling segitiga, rumus yang digunakan adalah jumlah panjang ketiga sisinya.

Contoh soal: Sebuah segitiga mempunyai panjang sisi a 6 cm, sisi b 8 cm dan sisi c 10 cm. Tentukanlah keliling dari segitiga tersebut!

Jawab: a + b + c = 6 + 8 + 10 = 24. Jadi, keliling segitiga tersebut adalah 24 cm.

Dengan mengetahui rumus luas dan keliling dari masing-masing bangun datar, diharapkan para siswa dapat mengerjakan soal matematika kelas 6 tentang bangun datar dengan lebih mudah. Penting bagi para siswa untuk selalu berlatih dan berusaha keras agar dapat menguasai materi dengan baik.

Karakteristik Bangun Datar Segitiga

Bangun datar segitiga adalah bangun datar dengan tiga sisi dan tiga sudut. Pada segitiga, sisi-sisinya menentukan sudut-sudutnya dan sebaliknya, sudut-sudutnya menentukan sisi-sisinya. Berikut adalah karakteristik bangun datar segitiga:

• Total Sudut: Jumlah total sudut dalam sebuah segitiga adalah 180 derajat. Ini berarti bahwa tiga sudut di dalam segitiga harus dijumlahkan dan selalu sama dengan 180 derajat.
• Tinggi dan Luas: Suatu segitiga memiliki tinggi dan luas, tergantung pada panjang alasnya. Alas segitiga adalah sisi yang tegak lurus dengan ketinggian. Ketinggian adalah garis yang ditarik dari sudut segitiga yang bersebrangan dengan alas ke sisi yang bersebrangan dengan sudut itu. Luas segitiga adalah setengah kali hasil kali alas dan tinggi.
• Jenis Segitiga: Segitiga dapat dibedakan berdasarkan panjang sisinya dan besarnya sudut. Segitiga sama sisi memiliki tiga sisi sama panjang, segitiga sama kaki memiliki dua sisi sama panjang dan sudut di antara sisi-sisinya sama besar, sedangkan segitiga sembarang memiliki sisi dan sudut yang berbeda-beda.

Karakteristik Bangun Datar Segiempat

Bangun datar segiempat adalah bangun datar dengan empat sisi dan empat sudut. Empat sisi pada segiempat dapat memiliki panjang yang sama atau berbeda. Berikut adalah karakteristik bangun datar segiempat:

• Total Sudut: Seperti halnya pada segitiga, jumlah total sudut dalam sebuah segiempat adalah 360 derajat. Ini berarti bahwa empat sudut di dalam segiempat harus dijumlahkan dan selalu sama dengan 360 derajat.
• Dua Pasang Sisi Sejajar: Dalam segiempat, ada dua pasang sisi yang sejajar. Artinya, kedua sisi tersebut sejajar dan memiliki panjang yang sama.
• Dua Sudut Siku-Siku: Seperti halnya pada persegi, segiempat dapat memiliki dua sudut siku-siku (90 derajat). Sudut-sudut siku-siku ini dapat diidentifikasi dengan mudah karena berada di berlawanan pada suatu sisi.
• Luas dan Keliling: Luas segiempat dihitung dengan mengalikan panjang alas dengan tingginya. Keliling segiempat dihitung dengan menjumlahkan panjang keempat sisinya.

Karakteristik Bangun Datar Lingkaran

Bangun datar lingkaran adalah bangun datar dengan radius sama pada setiap titik dari pusatnya. Dalam matematika, lingkaran sangat penting dan digunakan dalam banyak aplikasi. Berikut adalah karakteristik bangun datar lingkaran:

• Jari-jari: Jari-jari lingkaran adalah jarak dari pusat lingkaran ke titik mana pun pada lingkaran itu sendiri. Setiap lingkaran hanya memiliki satu jari-jari yang konstan.
• Diameter: Diameter lingkaran adalah jarak dua kali jari-jari. Setiap lingkaran hanya memiliki satu diameter.
• Luas dan Keliling: Luas lingkaran dihitung dengan mengalikan kuadrat jari-jari dengan bilangan pi (π), yang bersifat konstan (sekitar 3,14). Keliling lingkaran dihitung dengan mengalikan diameter dengan bilangan pi (π).

Lingkaran memiliki sifat unik: setiap titik pada lingkaran memiliki jarak yang sama dari pusatnya. Ini berarti bahwa tidak peduli di mana kita menarik dua titik pada lingkaran, jarak antara keduanya selalu sama. Sifat ini sangat berguna dalam aplikasi praktis, seperti membuat roda mobil atau piring.

Contoh soal dan penyelesaian bangun datar kelas 6

Matematika merupakan salah satu pelajaran yang sangat penting di sekolah dasar. Salah satu materi pentingnya adalah bangun datar. Bangun datar terdiri dari berbagai macam bentuk seperti segitiga, persegi, trapesium, dan masih banyak lagi.

Di bawah ini adalah beberapa contoh soal dan jawaban mengenai bangun datar untuk anak kelas 6.

Contoh Soal 1

Sebuah persegipanjang memiliki luas 24 cm2 dan keliling 20 cm. Hitung panjang dan lebar persegipanjang tersebut!

Penyelesaian:
Diketahui:

Luas = 24 cm2
Keliling = 20 cm
Ditanya: panjang dan lebar persegipanjang
Rumus:
Luas = panjang x lebar
Keliling = 2 x (panjang + lebar)

Maka:
24 = panjang x lebar
20 = 2 x (panjang + lebar)

Dari rumus ke dua, kita dapat mengubahnya menjadi:
10 = panjang + lebar
10 – lebar = panjang

Subtitusi ke dalam rumus pertama:
24 = (10 – lebar) x lebar
24 = 10lebar – lebar2
lebar2 – 10lebar + 24 = 0
Faktorkan! (lebih mudah)/mencari akarnya (leasing sulit)
(lebar – 6) x (lebar – 4) = 0

Dari sini kita mendapatkan bahwa lebar bisa bernilai 6 cm atau 4 cm. Jadi, panjang juga dapat dihitung dengan menggunakan rumus panjang = 10 – lebar. Hasil akhirnya adalah:
Panjang = 4 cm
Lebar = 6 cm

Contoh Soal 2

Sebuah segitiga memiliki alas 12 cm dan tinggi 8 cm. Berapakah luas dari segitiga tersebut?

Penyelesaian:

Diketahui:
Alas = 12 cm
Tinggi = 8 cm
Ditanya: luas segitiga
Rumus:
Luas segitiga = 1/2 x alas x tinggi

Maka:
Luas segitiga = 1/2 x 12 x 8
Luas segitiga = 48 cm2

Contoh Soal 3

Sebuah trapesium memiliki panjang sisi sejajar 10 cm dan 12 cm, tinggi trapesium adalah 8 cm, serta panjang sisi miringnya adalah 13 cm. Hitunglah luas trapesium tersebut!

Penyelesaian:

Diketahui:
Sisi sejajar 1 = 10 cm
Sisi sejajar 2 = 12 cm
Tinggi = 8 cm
Sisi miring = 13 cm
Ditanya: luas trapesium
Rumus:
Luas trapesium = 1/2 x (jumlah sisi sejajar) x tinggi

Maka:
Jumlah sisi sejajar = 10 + 12
Jumlah sisi sejajar = 22
Luas trapesium = 1/2 x 22 x 8
Luas trapesium = 88 cm2

Contoh Soal 4

Sebuah lingkaran memiliki jari-jari 7 cm, hitunglah keliling dari lingkaran tersebut!

Penyelesaian:

Diketahui:
Jari-jari = 7 cm
Ditanya: keliling lingkaran
Rumus:
Keliling lingkaran = 2 x phi x jari-jari (phi = 22/7 atau 3.14)

Maka:
Keliling lingkaran = 2 x 22/7 x 7
Keliling lingkaran = 44 cm

Dari keempat contoh soal di atas, dapat dipelajari rumus-rumus sederhana yang dapat digunakan untuk menghitung luas maupun keliling dari berbagai bangun datar yang ada, seperti persegipanjang, segitiga, trapesium, dan lingkaran. Dengan memahami materi ini dan melatih soal-soal seperti ini, diharapkan siswa kelas 6 dapat lebih memahami bangun datar dan meningkatkan kemampuan matematikanya.

Pentingnya Memahami Bangun Datar dalam Kehidupan Sehari-hari

Materi bangun datar merupakan pelajaran yang diajarkan kepada siswa Kelas 6 dan merupakan materi yang cukup penting. Bangun datar dapat ditemukan di berbagai objek dan kejadian sehari-hari. Oleh karena itu, memahami bangun datar sangat penting untuk diterapkan di kehidupan sehari-hari. Berikut adalah beberapa hal yang menjelaskan pentingnya memahami bangun datar dalam kehidupan sehari-hari.

1. Membantu dalam Menghitung Luas

Dalam kehidupan sehari-hari, terdapat banyak benda atau objek yang memiliki bentuk bangun datar. Contohnya seperti lantai, atap, meja, dan lain-lain. Dalam menghitung luas suatu benda tersebut, pengetahuan mengenai bangun datar akan sangat membantu. Dengan mengetahui rumus dan cara menghitung luas suatu bangun datar, kita dapat lebih mudah dan efisien dalam melakukan perhitungan.

2. Menghitung Volume dan Kapasitas

Tak hanya luas, pengetahuan mengenai bangun datar juga sangat membantu dalam menghitung volume dan kapasitas sebuah ruang atau objek. Dalam konteks kehidupan sehari-hari, pengetahuan ini sangat berguna untuk melakukan perencanaan, seperti menghitung kapasitas air dalam sebuah tempat penampungan, memperkirakan bahan yang dibutuhkan dalam mendesain suatu suvenir, dan lain sebagainya.

3. Mengembangkan Kemampuan Logika

Belajar bangun datar juga dapat memperkuat kemampuan logika seseorang. Pada dasarnya bangun datar terdiri dari beberapa bagian atau elemen dan masing-masing elemen tersebut mempunyai sifat dan sifat umum yang memudahkan seseorang dalam menganalisa dan memecahkan suatu masalah.

Dalam kehidupan sehari-hari, kemampuan logika adalah hal yang sangat penting dan berpengaruh dalam mengambil keputusan dan membuat solusi dari suatu masalah.

4. Meningkatkan Kreativitas

Bangun datar yang memiliki beragam bentuk dan sifat memungkinkan seseorang untuk lebih kreatif dalam mengaplikasikan pengetahuan tersebut dalam kehidupan sehari-hari. Contohnya, seseorang bisa menciptakan suatu karya seni seperti lukisan, tempat tidur, bahkan hiasan dinding menggunakan konsep-konsep bangun datar. Memahami bangun datar dapat menjadikan seseorang lebih inovatif dan berpikiran kreatif.

5. Menjadi Dasar bagi Pelajaran Matematika yang Lain

Memahami bangun datar adalah hal yang sangat penting dalam pembelajaran matematika selanjutnya. Misalnya, pada pelajaran geometri selanjutnya, banyak istilah-istilah yang membutuhkan pemahaman mengenai bangun datar.

Pemahaman yang kuat mengenai bangun datar akan memudahkan dalam menyerap dan memahami pelajaran matematika yang lebih kompleks di tahun-tahun berikutnya, seperti pelajaran matematika Kelas 7 tentang bangun ruang dan pelajaran matematika Kelas 8 tentang statistik dan peluang.

Dari kelima subtopik di atas, dapat dilihat bahwa pentingnya memahami bangun datar dalam kehidupan sehari-hari sangatlah besar. Maka dari itu, diharapkan siswa dapat memperhatikan dengan baik dan mencerna segala materi tentang bangun datar sehingga pengetahuan yang didapat dapat diterapkan di kehidupan sehari-hari dengan baik.